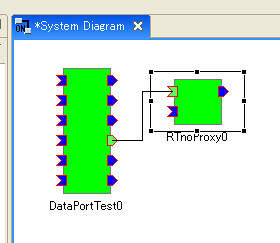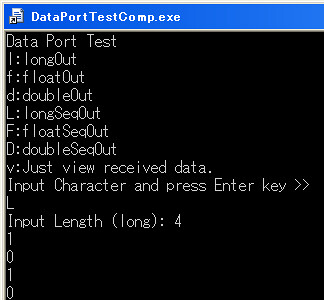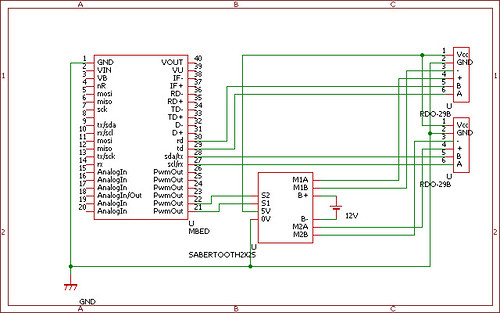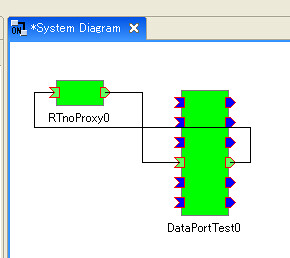
QPToolkitとは最近すっかり社会的認知度が高まっているARを行うためのライブラリから位置計測部分を抜き出した位置計測フレームワークです.
このフレームワークを利用することで,ごく普通のWebカメラから紙に印刷したマーカまでの距離姿勢を簡単に計測することができるのです.
カメラからマーカまでの3次元上の距離を計測するところまでは値を見るだけで簡単にできたのですが,姿勢を計測するのに結構手間取ってしまいました.
今回はそのことについて,もしかしたら超常識的なことなのかもしれないメモ書きです.
マーカの姿勢を取得するには回転行列+並進ベクトルで表されているOpenGLの行列というものを扱えばいいようです.
併進ベクトルはカメラからマーカまでの距離として,回転成分はなんぞや,と思って調べてみるとARマーカの回転成分はx-y-zオイラー角回転行列で示されているという文章を見つけました.
これは三次元の回転行列をx,y,z軸の順で回転させたもので,この形式の回転行列であるということがわかれば一応角度を取り出すことができます.
ここから先の計算に関してはこちらの下の方にそのものずばりが書いてありました.手で計算した後に見つけたって言う….
ここまでわかればプログラムに落とすことができますね.
processingで書いたものを以下に示してみます.プロトタイピングってことでとっても縦長です.すいません.
QPServer上で「Name」と「OpenGL model view matrix~」の二つにチェックを入れた状態で動かしてください.
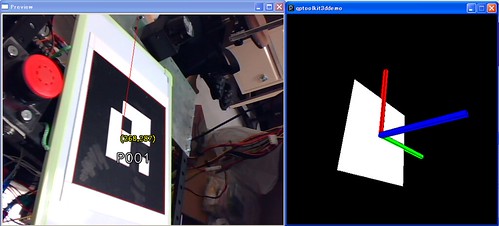
画面上に表示された3Dがカメラ上のマーカにあわせて傾いたり近づいたりするはずです.16cm四方のマーカならそのままで大丈夫ですが,それ以外のサイズだとマーカのサイズに合わせて表示位置や立体のサイズ変えないといけないかもしれません.
あとマーカを見つけたときだけ表示というようにしているせいか凄いちらつきます.画面から離れて部屋を明るくしてこのプログラムを利用してください.
import processing.net.*;
Client myClient;
double phi,theta,psi;
double X,Y,Z;
double[][] matrix = new double[4][4];
void setup() {
myClient = new Client(this,"192.168.145.1",55555); // IPとポート番号
size(480, 480, P3D);
frameRate(30);
}
void draw() {
background(0);
if (myClient.available() > 0) {
String dataIn = myClient.readStringUntil('\n');
if ( dataIn != null ) {
// "Num="を含むデータ列かどうかをチェックし,データ数を取得
if ( dataIn.indexOf("Num=")==0 ) {
int num = int(split(trim(dataIn),' ' )[1]);
// num個のマーカのデータを取得する
for (int i=0; i<num; i++) {
String marker_info = myClient.readStringUntil('\n');
if ( marker_info!= null ) {
// 1行分のデータを切り分けて欲しいデータを取得する
String[] data = split(trim(marker_info),',');
// マーカの名前と2次元座標
String name = data[0];
for(int m=0;m<4;m++)
{
for(int n=0;n<4;n++)
{
matrix[n][m] = Double.parseDouble(data[1+m*4+n]);
}
}
//傾斜角度を求める
if (matrix[0][2] > 0.998)
{
phi = Math.atan2(matrix[1][0],matrix[1][1]);
theta = Math.PI/2.0;
psi = 0;
}
else if (matrix[0][2] < -0.998)
{
phi = Math.atan2(matrix[1][0],matrix[1][1]);
theta = -Math.PI/2.0;
psi = 0;
}
else
{
phi = Math.atan2(-matrix[1][2],matrix[2][2]);
theta = Math.asin(matrix[0][2]);
psi = Math.atan2(-matrix[0][1],matrix[0][0]);
}
//併進ベクトルを代入
X=matrix[0][3];
Y=matrix[1][3];
Z=matrix[2][3];
println("X:"+X+" Y:"+Y+" Z:"+Z);
println("phi:"+Math.toDegrees(phi)+" theta"+Math.toDegrees(theta)+" psi:"+Math.toDegrees(psi));
println();
//マーカの位置にあわせて立体を表示
translate(width/2+(int)X, height/2+(int)Y,-(int)Z+600);
//軸の向き的にy軸に180度,z軸に90度回転させて表示.あとなんか-をかける.
rotateX(-(float)phi);
rotateY(-((float)theta+(float)Math.PI));
rotateZ(-((float)psi+(float)Math.PI/2));
//マーカ平面ぽいものを描画
stroke(0);
fill(255, 255, 255);
pushMatrix();
translate(-50, -50, 0);
rect(0,0,100,100);
popMatrix();
//X軸の棒を描画
stroke(0);
fill(255, 0, 0);
pushMatrix();
translate(-50, 0, 0);
box(100, 5, 5);
popMatrix();
//Y軸の棒を描画
stroke(0);
fill(0, 255, 0);
pushMatrix();
translate(0, -50, 0);
box(5, 100, 5);
popMatrix();
//Z軸の棒を描画
stroke(0);
fill(0, 0, 255);
pushMatrix();
translate(0, 0, 50);
box(5, 5, 100);
popMatrix();
}
}
}
}
myClient.clear();
}
}